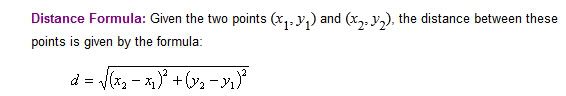|
 |
| View previous topic :: View next topic |
| Author |
Message |
Jochen Kochner
Joined: 08 May 2008
Posts: 10



|
| using float64 and cos; sin; acos and asin |
 Posted: Fri May 30, 2008 2:36 am Posted: Fri May 30, 2008 2:36 am |
 |
|
Hello,
I want to use the cos; sin; acos and asin function.
I'm using the datatyp float64 and a PIC24 with PCD compiler!
If I'm working with float values I get always wrong or inexactly results.
BUT the worse thing is that if I use the angle functions the other float calculations in the application, which works relative good, get completely wrong values back!
What's wrong?
What can I do?
I have changed the datatyp's (float32, float16 and float) without success!
thanks
Jochen |
|
 |
Ttelmah
Guest
|
|
 Posted: Fri May 30, 2008 4:29 am Posted: Fri May 30, 2008 4:29 am |
 |
|
Are you sure you understand that the angle functions in C, run in _radians_, not degrees?. So 'sin(1)', which on a normal desktop calculator would typically return 0.0174524064, in C, will return 0.84147098.
This is 'standard', for mathematics, since working in radians, is the 'norm' here, but is unintuitive to people used to 'everyday' operation in degrees.
Best Wishes |
|
 |
Jochen Kochner
Joined: 08 May 2008
Posts: 10



|
|
 Posted: Sun Jun 01, 2008 5:32 am Posted: Sun Jun 01, 2008 5:32 am |
 |
|
Thank you for your answer!
Yes, I know that I have to work with radians!
I have also an security check, that I don't use wrong values in the functions!
Regards,
Jochen |
|
 |
Ttelmah
Guest
|
|
 Posted: Sun Jun 01, 2008 3:01 pm Posted: Sun Jun 01, 2008 3:01 pm |
 |
|
OK. So what happens if you use 32bit float values?. Are the values then as expected?. I'd not put it past CCS, to have the 64bit libraries 'screwed, but the 32bit libraries are the same core code that has been around for a long while, and works pretty well. If the values are wrong with these, then you need to consider other possible sources for the problems (are you limiting input values to legitimate ranges for example?). If the faults only appear with the 64bit libraries, then I'm afraid you need to be talking directly to CCS.
Best Wishes |
|
 |
bill123
Guest
|
|
 Posted: Sun Jun 01, 2008 5:25 pm Posted: Sun Jun 01, 2008 5:25 pm |
 |
|
I am having the same problem. I think the problem is that precision is lost on each multiply in the math.h cos() algorithm. BTW, the source is provided for the cos() implementation (in math.h).
At this moment, I'm trying to "fiddle" with the factorial table values to improve accuracy. It appears that the author did this fiddling with the original implementation, as the values used in the table have been adjusted from the "correct" values. |
|
 |
Jochen Kochner
Joined: 08 May 2008
Posts: 10



|
|
 Posted: Mon Jun 02, 2008 1:26 am Posted: Mon Jun 02, 2008 1:26 am |
 |
|
Thank you very much for your answer!
Bill123, do you use also the PCD compiler (V4.073)?
Do you use also the cos() algorithm with the float64 datatyp? |
|
 |
sv_shady
Joined: 07 Mar 2008
Posts: 28


|
|
 Posted: Mon Jun 02, 2008 1:44 am Posted: Mon Jun 02, 2008 1:44 am |
 |
|
| If the arguments for cos and sin are relatively small finite number why dont you do a look-up table ? |
|
 |
Jochen Kochner
Joined: 08 May 2008
Posts: 10



|
|
 Posted: Mon Jun 02, 2008 2:16 am Posted: Mon Jun 02, 2008 2:16 am |
 |
|
| if there is no other solution, than I have to do so! |
|
 |
longtu
Joined: 15 Jun 2009
Posts: 6


|
|
 Posted: Thu May 03, 2012 2:26 am Posted: Thu May 03, 2012 2:26 am |
 |
|
Hi Jochen Kochner,
I have the same problem when to use sin(), cos(), acos()...in CCS. Did you have a solution for this?
Thanks for your answer quickly. |
|
 |
RF_Developer
Joined: 07 Feb 2011
Posts: 839


|
| An old thread |
 Posted: Thu May 03, 2012 5:07 am Posted: Thu May 03, 2012 5:07 am |
 |
|
Longtu: this is digging up a thread that's four years old...
Technically its not possible to *precisely* compute sine(x), nor any of the trigonemtrical functions. No computations can give the "right" answer, all computations are approximations. The question is how accurate the approximations are.
There are many ways to compute the trig functions. Currently CORDIC based methods appear to be the most commonly used in hardware. In pure software implentations other methods are more appropriate. All are approximations, and trade-offs between accuracy, speed and code size. From what little I can see, and in this CCS is *very* unusual in allowing us to see how it computes these functions, the CCS C version is fairly "simple". The coefficients are probably optimised for general use, this means that gives reasonable results over the full range if values, but could be optimised to give better results over smaller specific ranges. I cannot say, without lengthy testing and processing, if the results are as good as they "could be". Nor would I advise fiddling with the constants in the hope of getting "better" results.
I was taught to use Chebychev approximations, and indeed inspection of the output of a real compiler (for ALGOL 60!) showed me that yes, that's what is must have been using. The primary advantage was that by using carefully selected constants the series could be shorter, and thus faster, than the naive version, *for a given precision*. That was in the days when speed was the critical issue... and the memories were tiny by today's standards.
http://www.ganssle.com/approx/approx.pdf gives a useful discussion of the constants with examples for various precisions.
http://earthlingsoft.net/ssp/blog/2008/01/sine_computations shows that the precision of hardware is not consistent either! There is no "standard" comuptation that gives the "right" result, they are all approximations, and "rightness" is in the eye of the beholder.
RF Developer. |
|
 |
longtu
Joined: 15 Jun 2009
Posts: 6


|
|
 Posted: Thu May 03, 2012 6:22 am Posted: Thu May 03, 2012 6:22 am |
 |
|
Dear RF_Developer,
That is a big help. Thank you very much with your explaination. Now, I know that all trigonemtrical functions will be received the approximations result. BUT I need the the near "right" answer for my application below:
Application: Calculator Distance Between 2 coordinates:
My code:
| Code: |
/////////////////////
float distance(float lat1, float lon1, float lat2, float lon2, char unit)
{
float e=(3.1415926538*lat1/180);
float f=(3.1415926538*lon1/180);
float g=(3.1415926538*lat2/180);
float h=(3.1415926538*lon2/180);
float i=(cos(e)*cos(g)*cos(f)*cos(h)+
cos(e)*sin(f)*cos(g)*sin(h)+
sin(e)*sin(g));
float j=(acos(i));
float k=(6371*j);
return k;
}
////////////////////
|
This code only run well if the distance between over 10Km. I tested and checked with this wedsite below:
http://andrew.hedges.name/experiments/haversine/
- Point 1: (lat1,lon1)= (0.1,0)
- Point 2: (lat2,lon2)= (0,0)
My code reponse: 10.7755360km(it is near 11.123 km reponse from website.
If the distance less than 10km, my code allways reponse 0 km.
I found the error is: i >= 1(always) therefore j=(acos(i)) = 0 -->distance= 0
I checked with excel, the result is very good: see more pictures below:
Code:
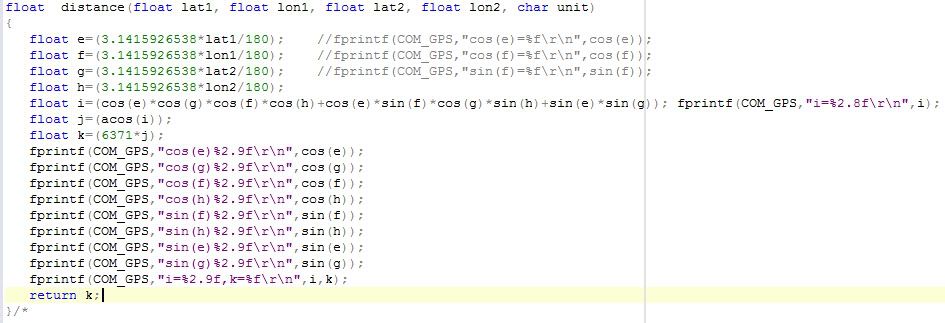
CCS compare with Excell:
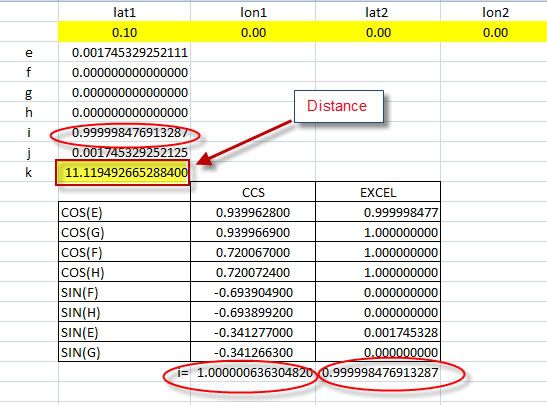
Please help me to improve this results.
Thanks.
_________________
----------------------------------------------------------
[email protected] |
|
 |
Douglas Kennedy
Joined: 07 Sep 2003
Posts: 755
Location: Florida



|
|
 Posted: Thu May 03, 2012 9:01 am Posted: Thu May 03, 2012 9:01 am |
 |
|
| Real Estate is location, location and location. The math equivalent is notation, notation notation. The Babylonians used base 60 we commonly use base ten and PIC's use base 2 notation. The math being used is based on the unit circle where sin(0) is 0 and cos(0) is 1.This is true whether you're a Babylonian or a PIC. This is very useful in that the fundamental functions return values contained inside the unit circle and further are contained by multiplication. Less than 1 times less than 1 is less than 1. Now the COORDIC is in binary notation so it is accurate within that base ( and can be extended to arbitrary precision but care is needed at quadrant boundaries decimal 0, 90 ,180 360 deg and further the notation transfer to decimal has a constant of proportionality as well as the regular binary to decimal notation transfer issues. To a space probe it doesn't matter what the notation is so staying in binary is just fine but to us mortals with Excel spread sheets we like our decimal notation to be just so. We however can never get close enough.. a handheld calculator uses base ten so it looks neat.. A PC can use extended 64 bit and it looks neater the PIC can do the same but is is slooooow. I'd go with a look up table sin cos in binary that breaks the degrees into finite increments ex 1/10 of a degree use 32 bit integer math with an assumed leading decimal point. |
|
 |
Ttelmah
Joined: 11 Mar 2010
Posts: 19553


|
|
 Posted: Thu May 03, 2012 9:23 am Posted: Thu May 03, 2012 9:23 am |
 |
|
Do a search here, using the keyword 'Haversine'.
This is a formula, that was originally specifically designed to give good 'distance between co-ordinate' results, for systems with limited accuracy sin/cosine functions. It has been proposed here on many occasions to people doing exactly your calculation.
It gives results to a small fraction of a km, even using the Float32 code.
Best Wishes |
|
 |
RF_Developer
Joined: 07 Feb 2011
Posts: 839


|
|
 Posted: Thu May 03, 2012 9:58 am Posted: Thu May 03, 2012 9:58 am |
 |
|
See the thread, http://www.ccsinfo.com/forum/viewtopic.php?t=47980, where this topic was discussed in some depth, including recommending the Haversine method.
By the way, even Excel is not "right" i.e. precise, and its results will vary with processor!
RF Developer |
|
 |
longtu
Joined: 15 Jun 2009
Posts: 6


|
|
 Posted: Thu May 03, 2012 11:07 am Posted: Thu May 03, 2012 11:07 am |
 |
|
Thanks for your all answer.
I think this problem cause by all trigonometrical functions will be answer approximations value. And limits of digit by float type in CCS.
Here is my solution for my application(Calculator distance between 2 coordinates):
Step 1: Corvert GPS coordinate(ddmm.mmmmmm) to decimal degrees(dd.dddddd):
| Code: |
float gpstogoogle (float gps)
{
int16 degrees = (int32) gps / 100;
delay_us(50);
float minutes = gps - 100 * degrees;
return (degrees + minutes / 60.0);
} |
Note: We can use this decimal degrees to find coordinates in http://www.google.com/maps
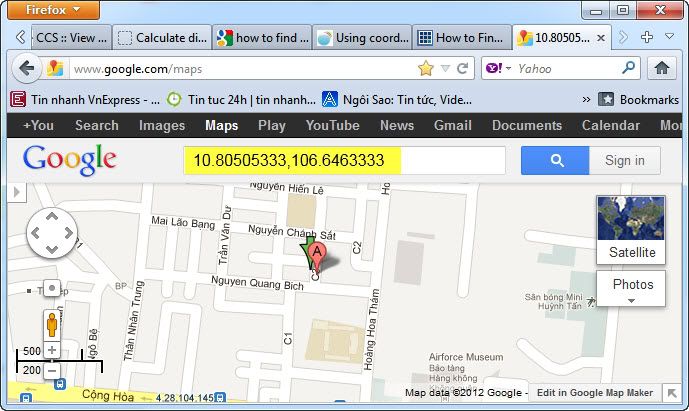
Step 2: Calcular distance between 2 coordinates:
- Distance fomula:
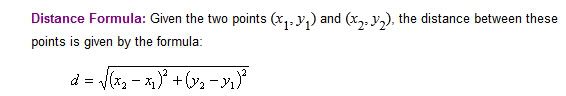
- Note that: 1° ~ 111.123km
- My code:
| Code: |
#define OffetDist 111.123
//1° ~ 111.123km
float distance(float lat1, float lon1, float lat2, float lon2)
{
float dist;
dist= OffetDist * sqrt(pow((lat1-lat2),2)+pow((lon1-lon2),2));
//return (dist);//Km
return (dist*1000);//Meters.
} |
This is very sample but excellent results.
The wedsite could be uesed for testing:
http://www.daftlogic.com/projects-google-maps-distance-calculator.htm
_________________
----------------------------------------------------------
[email protected] |
|
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
|
Powered by phpBB © 2001, 2005 phpBB Group
|